【印刷可能】 円 中心 求め 方 801635

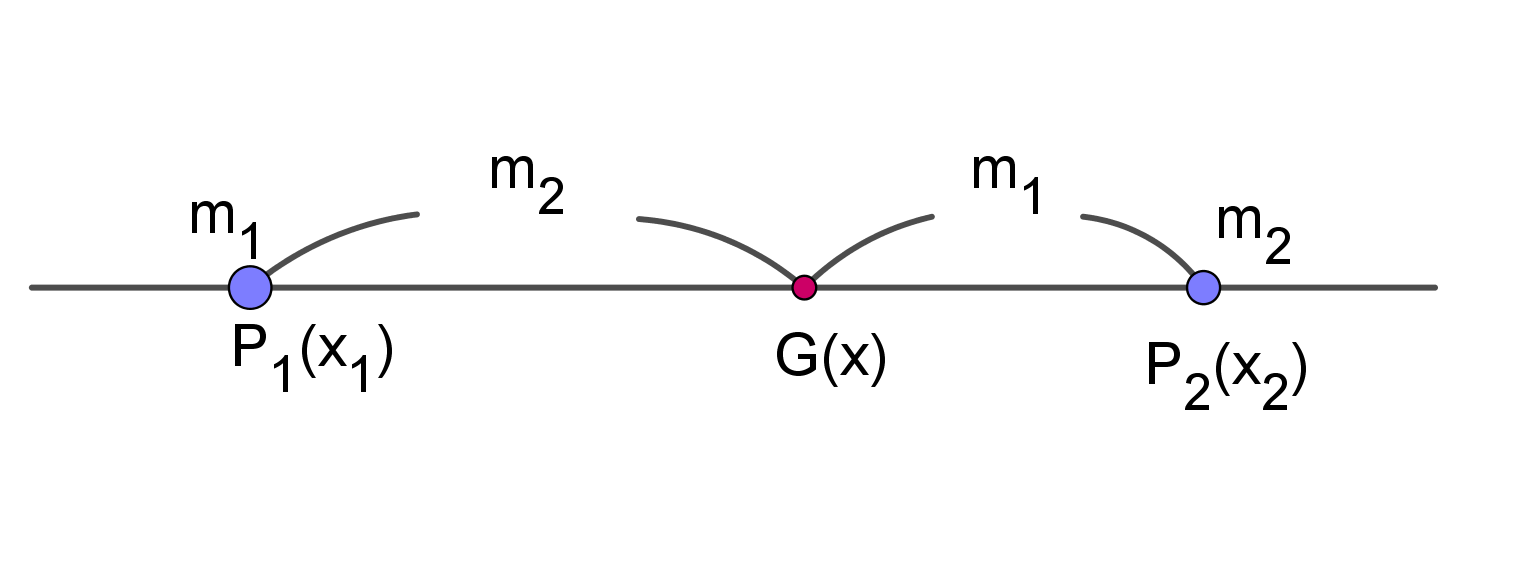
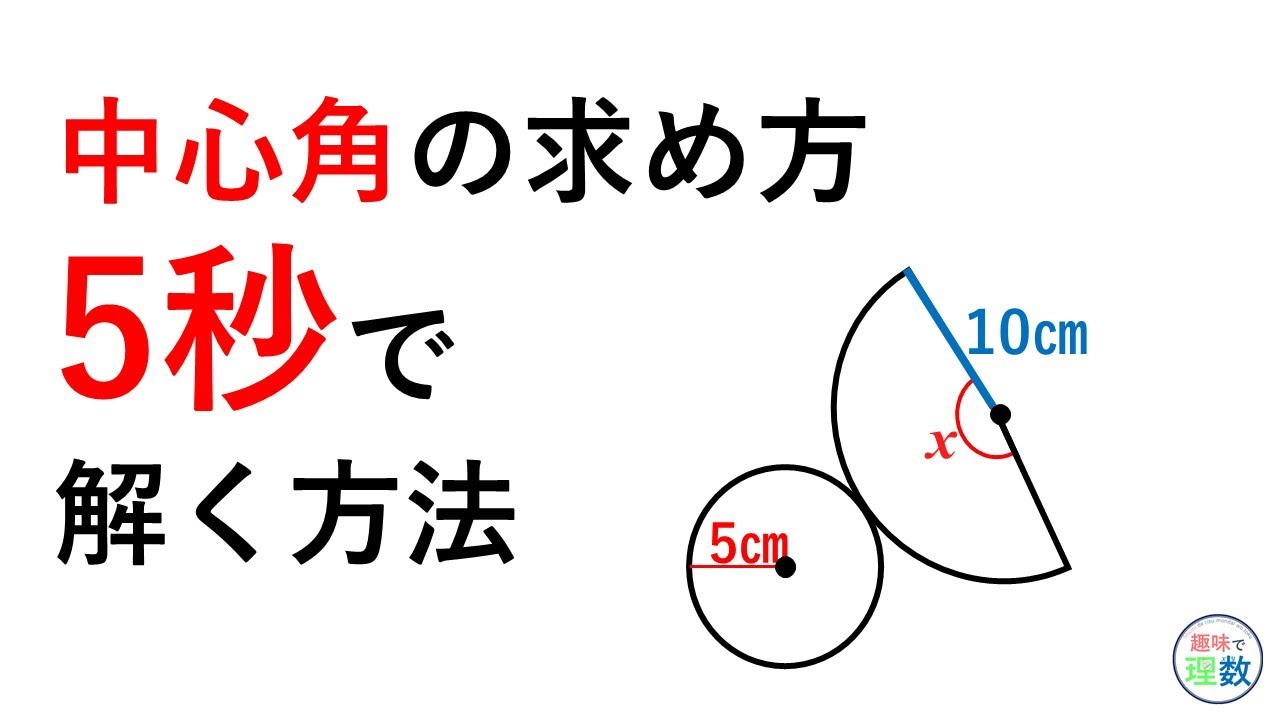
中心角の作り方がわかったところで、もう一回先ほど定義を見てみましょう。 円の中心核の定義は、 「弧の両端を通る2つの半径の作る角」 でしたね。 この「2つの半径の作る角」のところは、②と③で確認した部分のことです。Xは3コマ分の中心角の半分 (=円周角) → x = 1 2 1 2 (3×45°) = 135°空き缶の中心の見つけ方 1、空き缶の円を紙に写し取ります。 直角の物（ハガキなど）を置きます。 （Pの位置） 3、直角の物と円が交わる2点に印を付けます。 （AとB） 4、AとBを結んだ線の真ん中の点が、この円の中心になります。 （Oの点） 5、紙を空き缶に乗せて、求めた円の中心をクギなどで印を付ければできあがり！

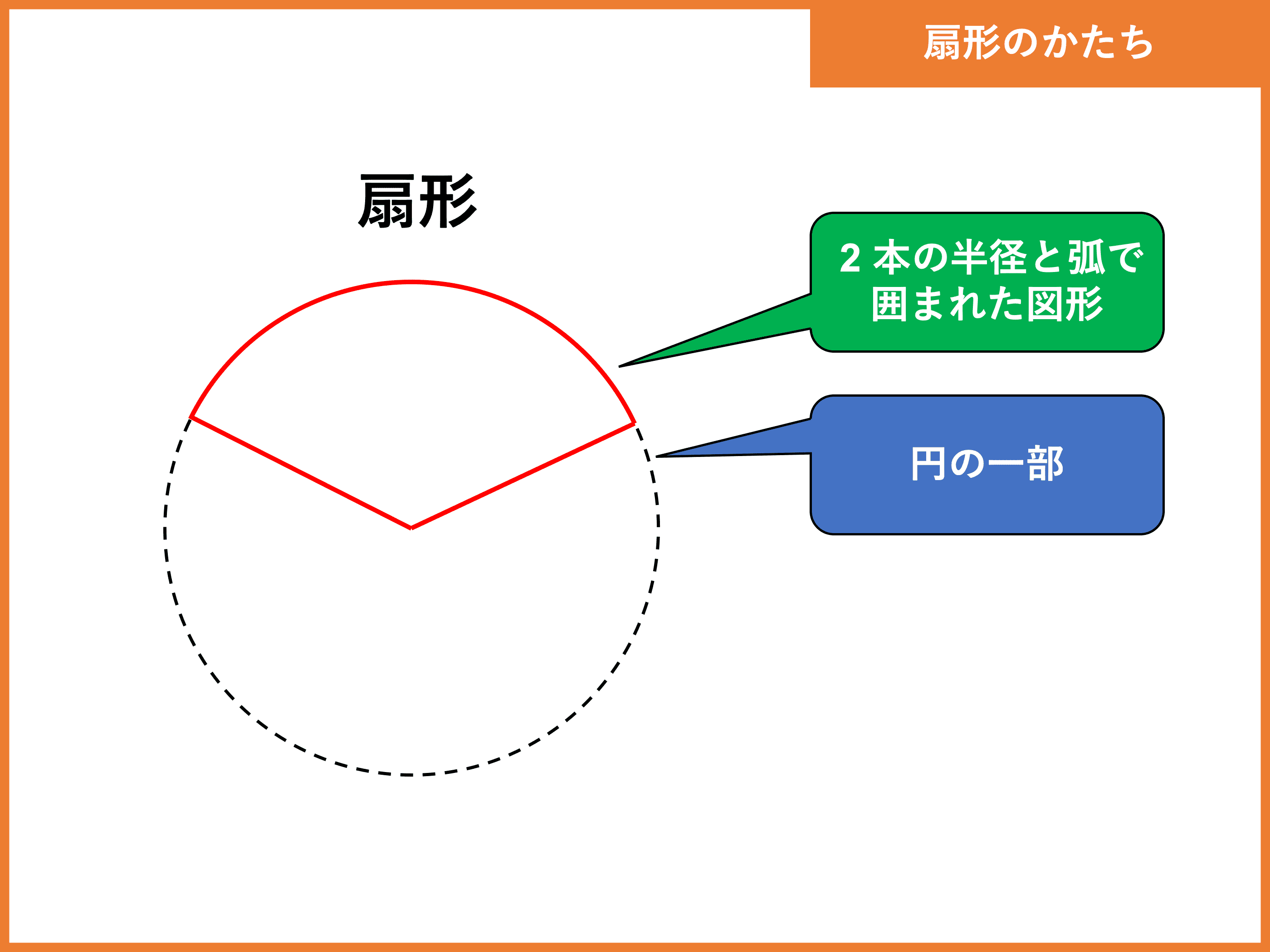
扇形 面積 求め 方

円 中心 求め 方

円 中心 求め 方-円の中心点のもとめかた 焦点をf,f'とすると 「ff'の中点は楕円の中心」で合っていますか。 数学 10 楕円の焦点の求め方多数 (4～16個)の座標データから、円の直径が最小となる3点を見つけ、中心座標と直径を求めたい (エクセルで) アンケートにご協力頂き有り難うございました。 送信を完了しました。 三角形の外接円 のアンケート記入欄 性別 男 女 年齢 歳未満

円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典

基本円と直線の共有点（二次方程式に注目）と同じ設定ですが、共有点の個数だけなので、上で見た内容を使いましょう。 円の中心は原点で、半径は $\sqrt{2}$ です。原点と各直線との距離をそれぞれ求め、半径と比べましょう。3点を通る円POINT 円の通る3点から中心・半径を求める一般式を導出する． 導出した式で計算フォームを作成． Excelにコピペして使えるフォーマットあり． 単純な「連立方程式」の問題ですが，一般解は少し複雑な形になります． 計算フォーム Excel用フォーマット 導出 円の方程式 円の中心 円同様に、yは2コマ分の中心角の半分 → y = 1 2 1 2 (2×45°) = 90°

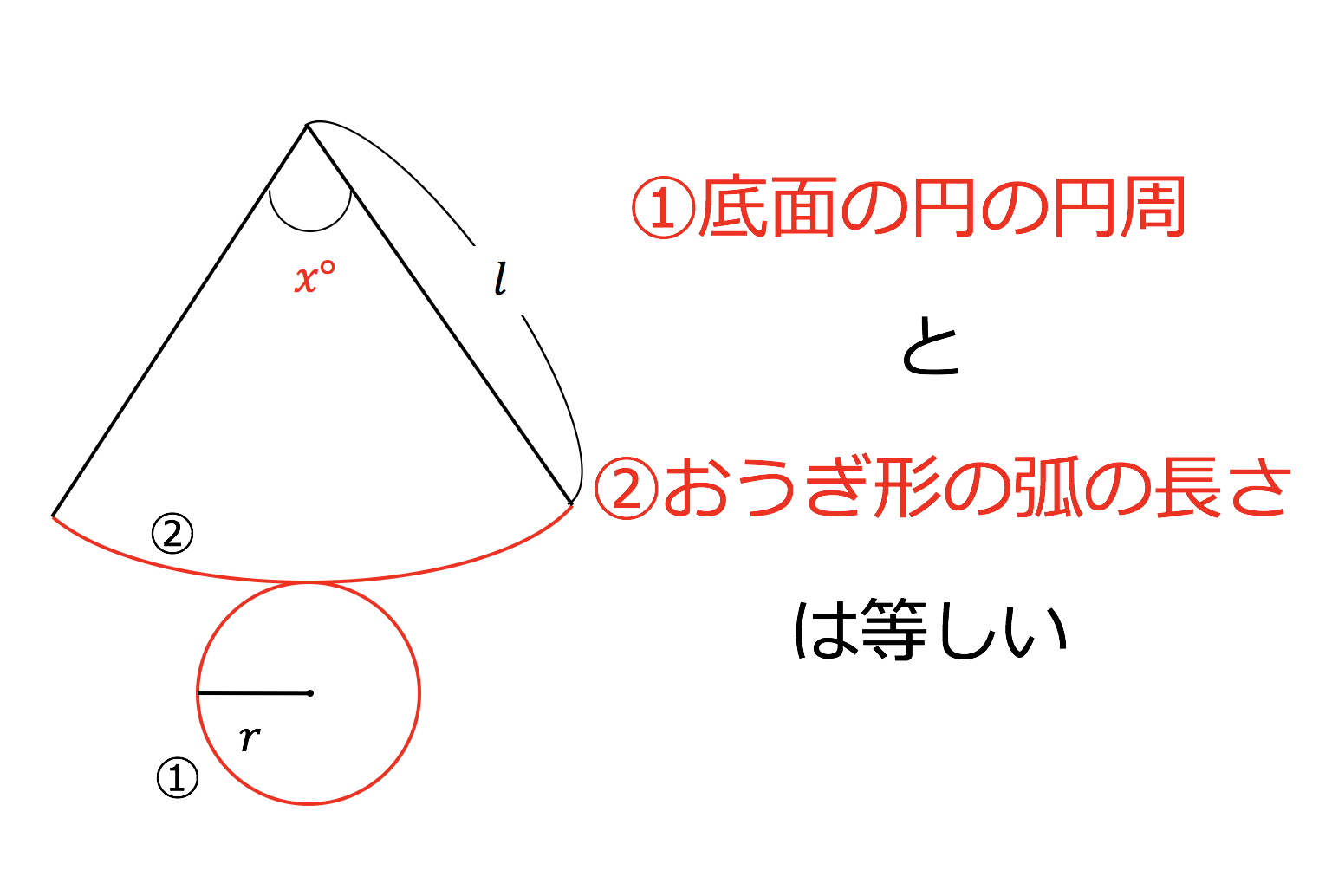
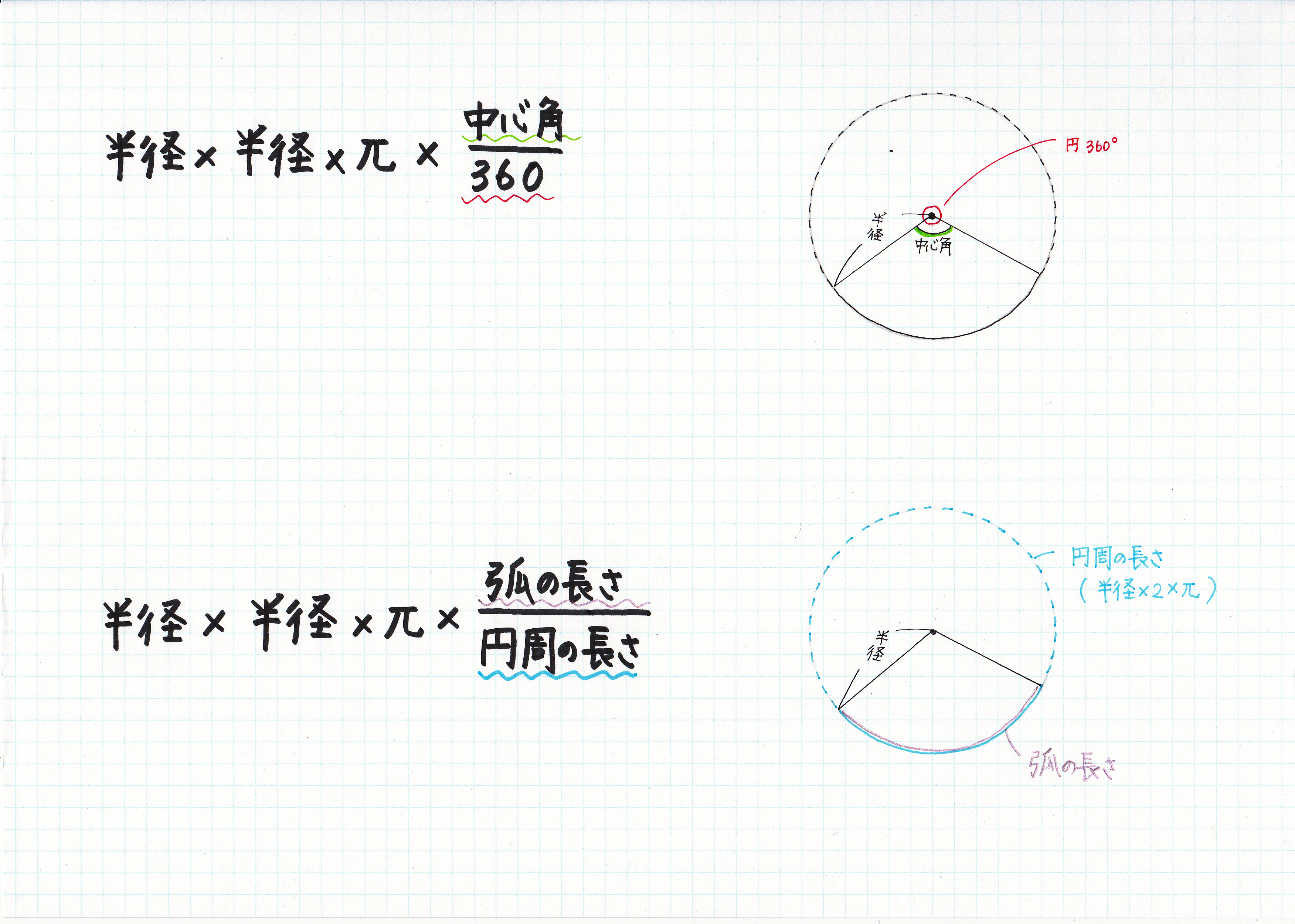
すなわち，上記の偏心（a,b）を決定し，それを中心と した同心円でワーク形状を挟んだ場合の半径差が真円度と なることを意味している． 5．真円度と基準円 真円度の求め方には，基準円を元に以下の4つの方法が ある3)． 1．最小領域真円度／最小領域基準円円周を8等分した点です x, y, z の角度を求めましょう →1コマあたりの中心角は 360°÷8 = 45°円の円周と扇の弧の長さは等しい 円錐の中心角の求め方は、 扇部分の半径・弧の長さを求める (扇の中心角を求める問題になる) 中心角を求める はかせちゃん 今日もお疲れ様でした！ 抹茶ラテ飲んでゆっくりしましょ～ 関連記事はこちら 中学数学

A 外心を (a,b),半径をRとして「 外心から頂点までの距離が等しい 」条件を立式する。 b 各辺の 垂直二等分線の交点 であることから垂直二等分線を立式する。 aが最もわかりやすいと扇形 ～弧の長さ、半径から中心角を求める～ 実行数 円の半径 中心角 °;こちらの面では中心を出せないので、 まずは紙コップを逆さにします。 紙コップのこちらの面を使って 紙コップの円の中心を出して行きます。 紙コップの円の中心を出す時に使う道具がコレ。 L型サシに45度の三角定規です。 L型サシがなければ

03 号 ダクトの真円度 真直度計測システム Astamuse

外接円内の点かどうかを調べる Qiita

例として，中心が (0, 0) (0,0) (0, 0) で半径が 2 2 2 の円の方程式を考えます。このように 「原点が中心の円」 で 「接点が ( x 1 − a, y 1 − b) である接線の方程式」 を考えることになります。 ここがミソです。 そうすると先ほど私たちが覚えた接線の公式が使えて ( x 1 − a) x ( y 1 − b) y = r 2 とできますね。 あとは 円を元の位置っていう計算式が公式としてのっているね。 たとえば、直径3cmの円があったとすると、円周の長さは、 3 ×

三角定規で円の中心を作図 おときち副塾長 電脳空間学習塾かもん Youtube

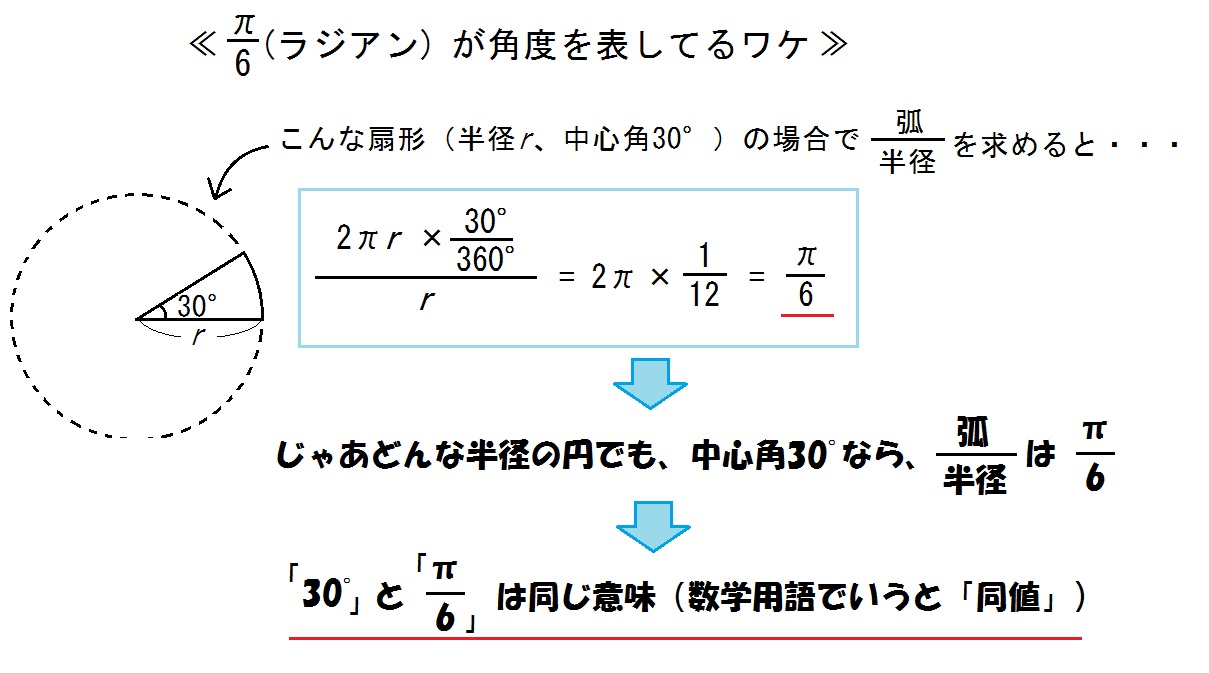
扇形 中心 角 求め 方 扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ

円の上で 右クリック して、そのまま3時方向にドラッグします。 クロックメニューが現れたら、マウスボタンを放すと中心点が表示されます。。 ※ ドラッグとは マウスのボタンを押さえたまま、マウスを移動させる操作のことです。では，円の方程式の導き方を確認しましょう。 ここでは， 『「円周上の点」と「中心」の距離』と『半径』が同じ ということを利用して，円の方程式を導いてみます。 さらに，この式を展開して整理すると， x2 y2 2 ax 2 by a2 b2 r2 =0 となります。 これより，円の方程式は l，m，n を定数として， x2y2lxmyn=0・・・・・・ (2) （円の方程式は， (1)や (2)の形で球の中心の求め方 前回のコラムで3次元空間での円の中心の求め方について記述したので、次に空間内にある球の中心を求めるロジックについて考えてみます。 球については、表面上にある4点の座標が指定されたら形状が確定します。 （3点の座標と半径

1997 2148号 同心円傾向画像中心算出方法 Astamuse

中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

3点を通る円 円は一直線上ではない3点の座標があれば一意に決定します。 下図を参照してください。ここで、3点の座標を、 (x1, y1), (x2, y2), (x3, y3) 求める中心座標を、 (Cx, Cy) 求める半径を、 r とします。求める円の中心は、\((−2, 0)\) と \((1, 0)\) の中点なので、 \(\displaystyle \left( \frac{−2 1}{2}, \frac{0 0}{2} \right) = \left( −\frac{1}{2}, 0 \right)\) 直径が \(3\) なので、半径は \(\displaystyle \frac{3}{2}\) ゆえに、円の方程式は \((x − a)^2 (y − b)^2 = r^2\)まず、内接円の中心（内心）を求めます。 性質②から、 角の二等分線の交点 を求めればよいですね。 角の二等分線は、各頂点からコンパスをとって弧を描き、弧と辺が交わる \(2\) 点からさらに弧を描き、その交点と頂点を直線で結べば作図できます。

1数 作図による円の中心の求め方 Youtube

3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ

2つの点から円の方程式を求める問題 2点A（2，3）とB（4，－3）を直径の両端とする円の方程式を求めなさい まずは図を描いてみましょう 考え方 AとBが直径の両端ということは、ABが円の直径 円の方程式を求めるためには、円の中心もしも， が円弧だとすれば，円の中心を ， ，円の半径を として， がなりたつはずです（次図）．円弧の長さ，中心角が分かっていて，半径を求めたいのなら次のような形にしておけば良いでしょう． （中心角が になることは，ちょっと考えれば分かります．）右図5において，原点を中心とする半径5の円の方程式を求めてみよう． 円周上の点 P の座標を (x , y) とおくと，ピタゴラスの定理（三平方の定理）により， x 2 y 2 =5 2 (A) が成り立つ． 上半円については， y ≧ 0 なので， y= (B)

円の中心角の求め方を教えてください よろしくお願いします Clear

50 おうぎ形 中心角の求め方 公式 最高のぬりえ

平方完成ができたら、残りモノは右辺に移行しましょう。 最後に右辺を 〇 の形に変形すれば 完成！ この式の形から このように中心と半径を読み取ることができました！ 円の中心と半径を求めるためには、平方完成して式変形する！ ということでしたね。 手順を覚えてしまえば簡単です (^^) それでは、解き方の手順を身につけたところでもう1問だけ解説して中心の座標が (x0, y0) 半径 r の円 (x − x0)2 (y − y0)2 = r2 と、直線 ax by c = 0 の交点を求める。 上記求め方の考え方により、まずベクトル → CH, → HA を求める必要がある。円の中心点を簡単に出す使い方 円の中心点を求めることも図面作成中によくあることだと思います。 円の中心点を出すのは、以外と難しいものでそう簡単には出すことができません。 しかし、Jw_cadなら数クリックで簡単に出すことができる機能が備わっています。 今回はその機能を使って簡単に円の中心点を出す使い方の練習です。

極方程式まとめ 直線 円 面積公式 理系ラボ

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

坂田繁洋 17年4月3日 三角形の中心で、数学を学ぶ T 研究コラム 数学 三角形は紀元前から研究されている最も基本的な図形です。 私たちは、小学校・中学校・高等学校において、三角形の多くの性質を学んできました。 しかし、三角3次元空間での円の中心の求め方 年6月12日 / 最終更新日時 年6月12日 iNak Eng CEO VBNet 前回のコラムがくだけすぎでしたので、今回はまともなロジックを取り上げます。外接円、外心について 「外接円」や「外心」の用語や意味は中学の 教科書の発展内容としてあります。 それぞれの各辺の垂直二等分線は一点でまじわり、その点Dを中心に円を書くと Dを中心に三角形の3つの頂点を通る円を書くことができて、この円

中1 数学 中1 平面図形 中学生 数学のノート Clear

おう ぎ 形 中心 角 求め 方 扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト

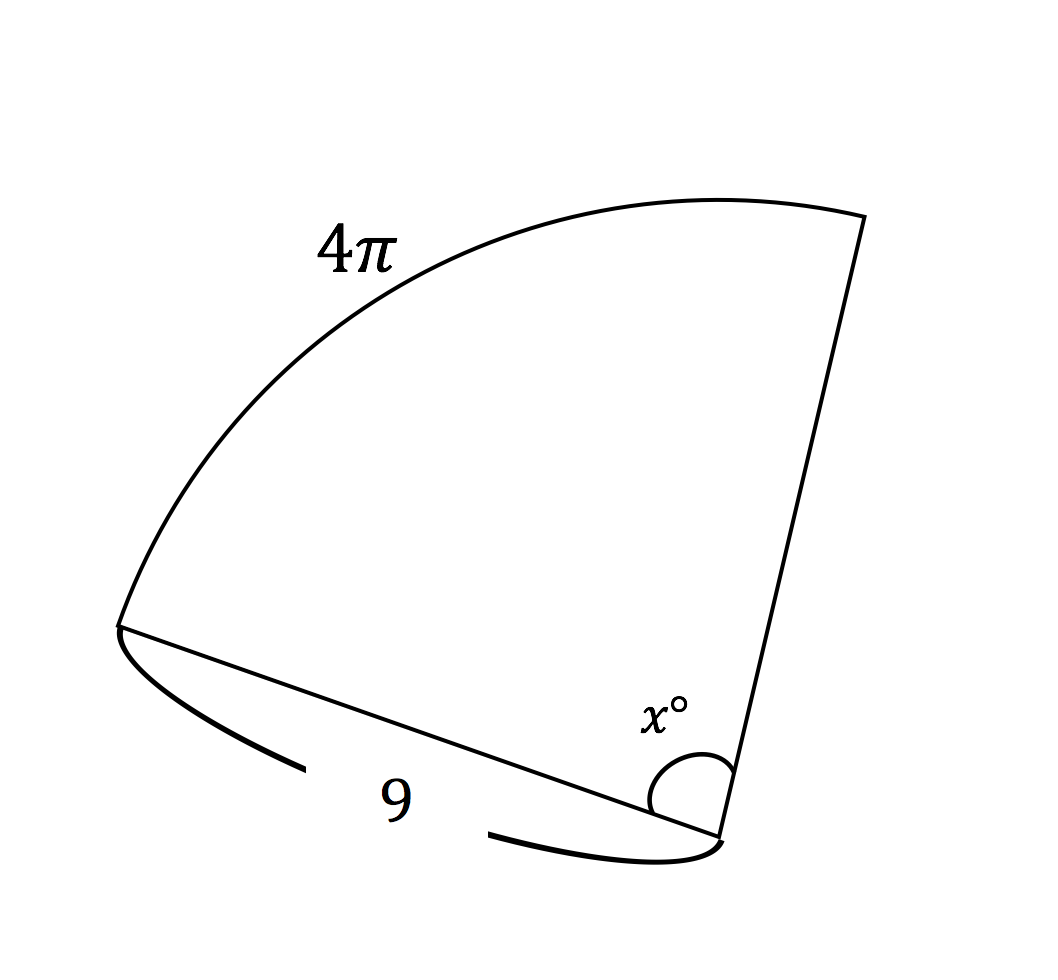
三点を通る円の中心座標と半径を求める公式を教えてください。ちなみに3点はa（－4,3） b(5,8) c(2,7) です。高校の頃にやった覚えがあるのですが、現在大学4年になりまして、すっかり忘れてしまいました。どなたか知っている方がいら314 = 942 cm

おう ぎ 形 中心 角 求め 方 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる

Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary

3点を通る円の中心と半径 Notes Jp

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

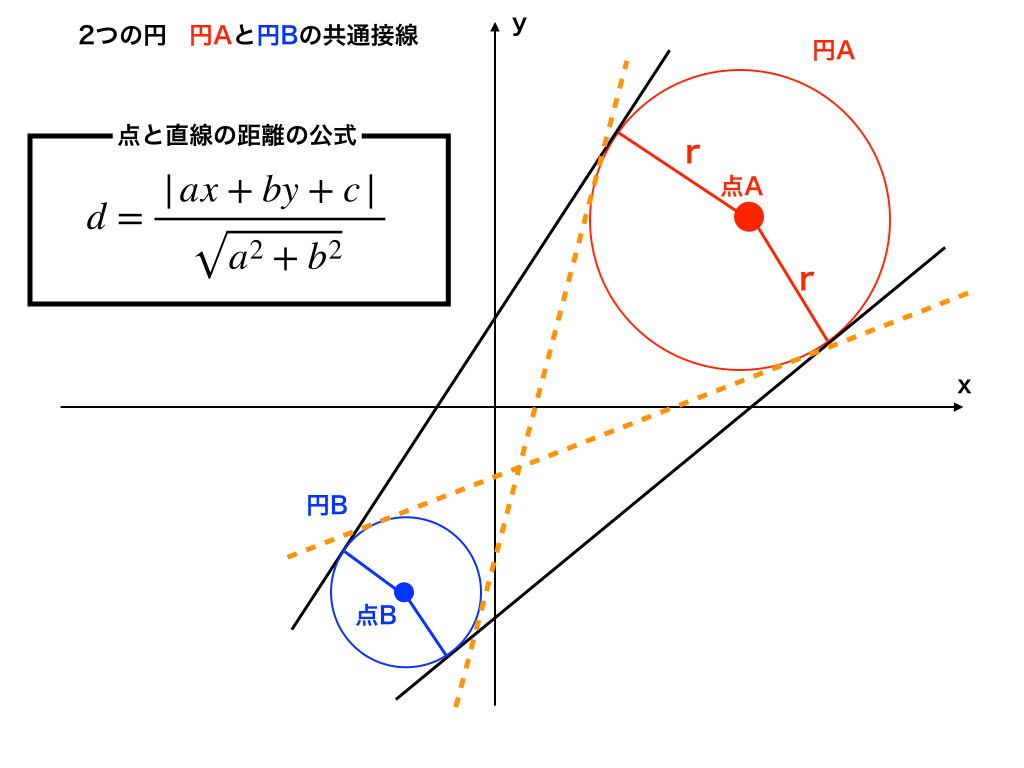
2つの円の位置関係と共通接線の求め方 図形と方程式 2

高校数学 ２つの円が接する条件 例題編 映像授業のtry It トライイット

いろいろな正多角形をかいてみよう 家庭学習レシピ

Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary

円周の求め方

球面の方程式の求め方と問題の解き方をわかりやすく

扇 型 面積 円 扇形 の面積 周や弧の長さの公式 数学fun

高校受験数学 円とおうぎ形 中心角の求め方 方程式編の授業映像 プリント無料配布 Youtube スタディカフェ

扇形 中心 角 求め 方

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

9div2 Descubre Como Resolverlo En Qanda

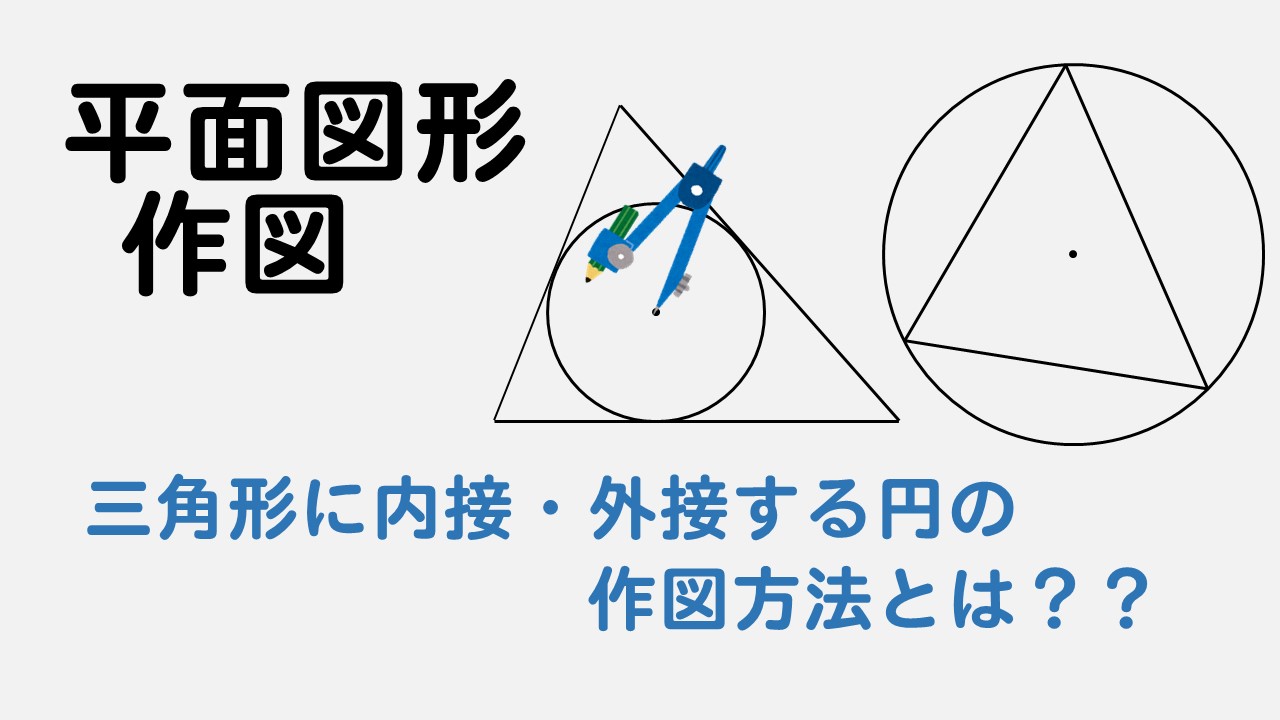
作図 三角形の内接円 外接円のかき方をポイント解説 数スタ

3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ

内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ

円 周 の 求め 方 ピクチャー ニュース

おう ぎ 形 中心 角 求め 方 扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト

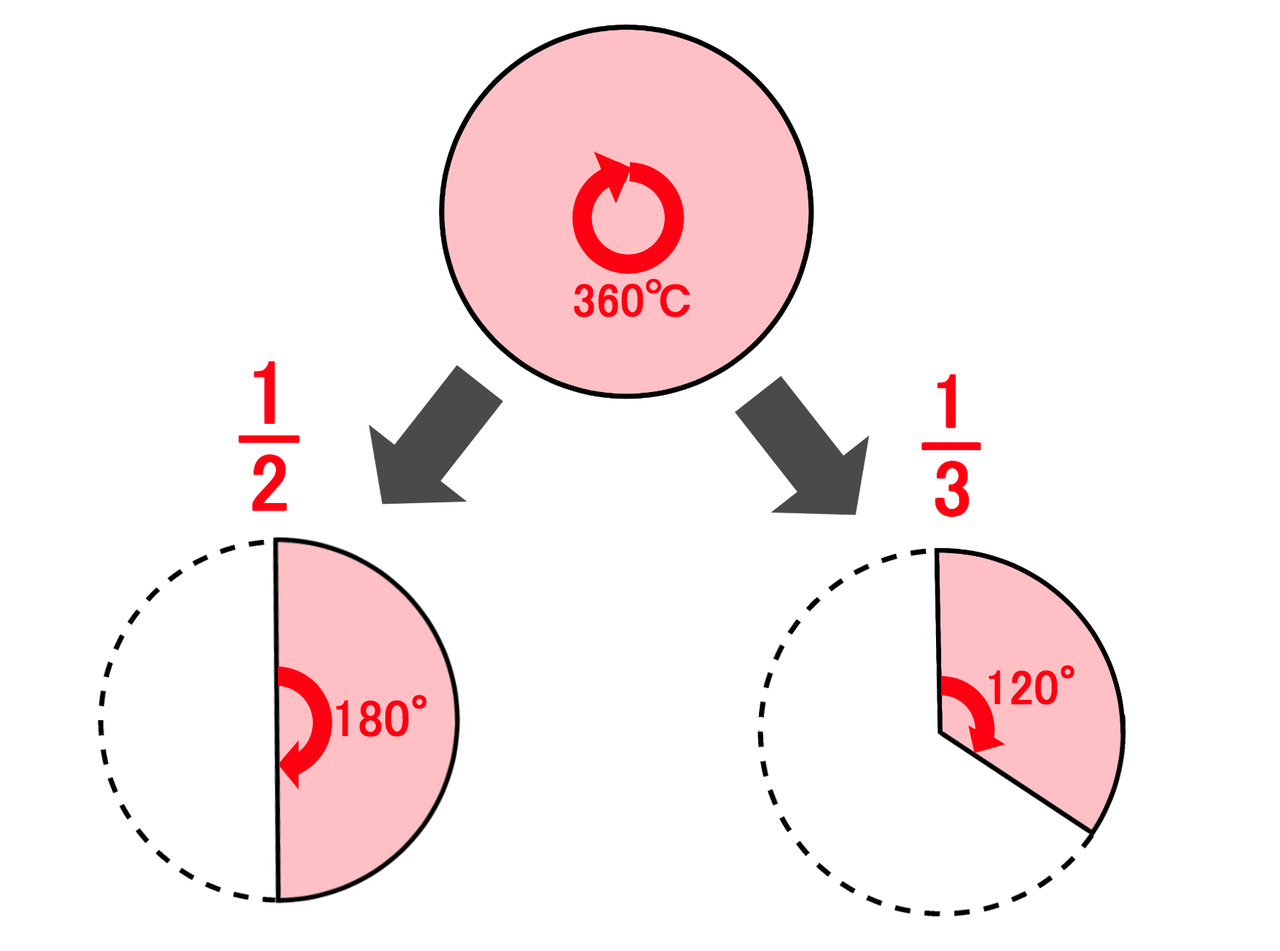
おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学

中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく

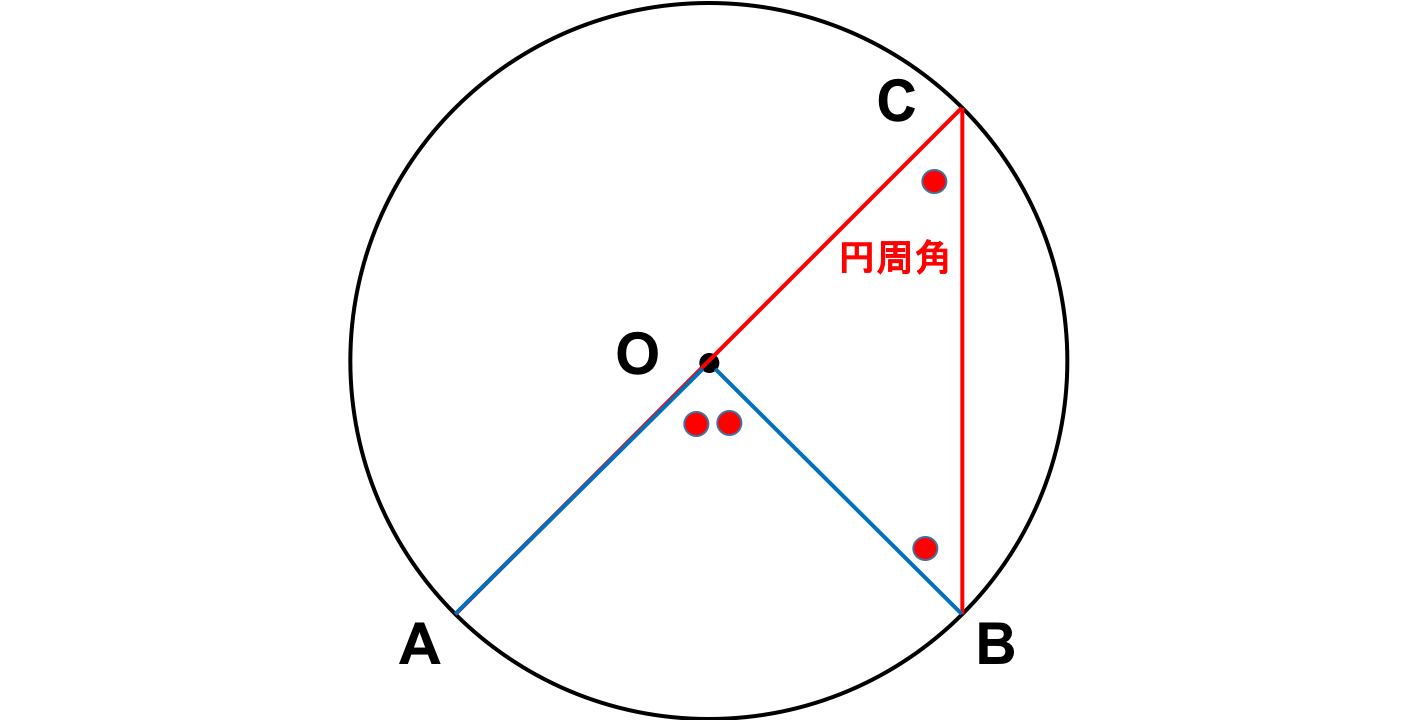
円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest

円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典

おう ぎ 形 中心 角 求め 方 扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト

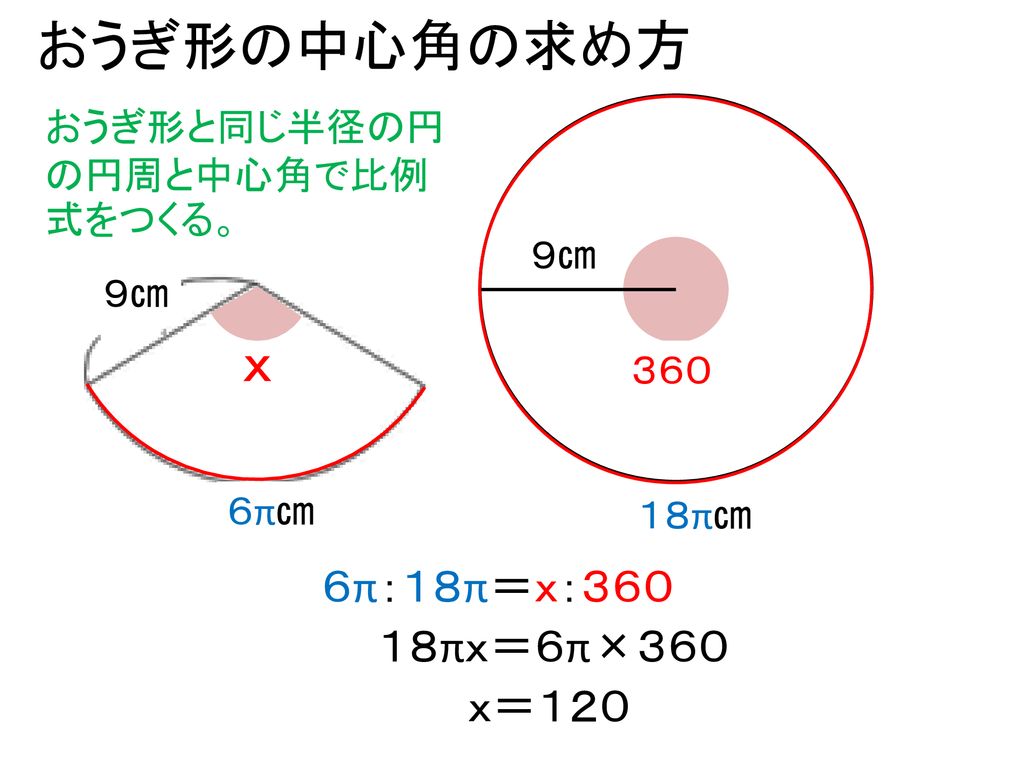
おう ぎ 形 中心 角 求め 方 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる

おう ぎ 形 中心 角 求め 方 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる

My Math Note

扇形 中心 角 求め 方

扇形 中心 角 求め 方

とにかく涼しく パワーを求める方にオススメ 正規品 パワーファンスターターキット 大容量バッテリー 急速ac充電アダプターセット ファンセット 空調服 ジーベック Sksp01 Xebec 割り引き 熱中症対策 冷却 ファン付 扇風機 涼しい

内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ

6 の作図がこのようになるのですが Clear

円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典

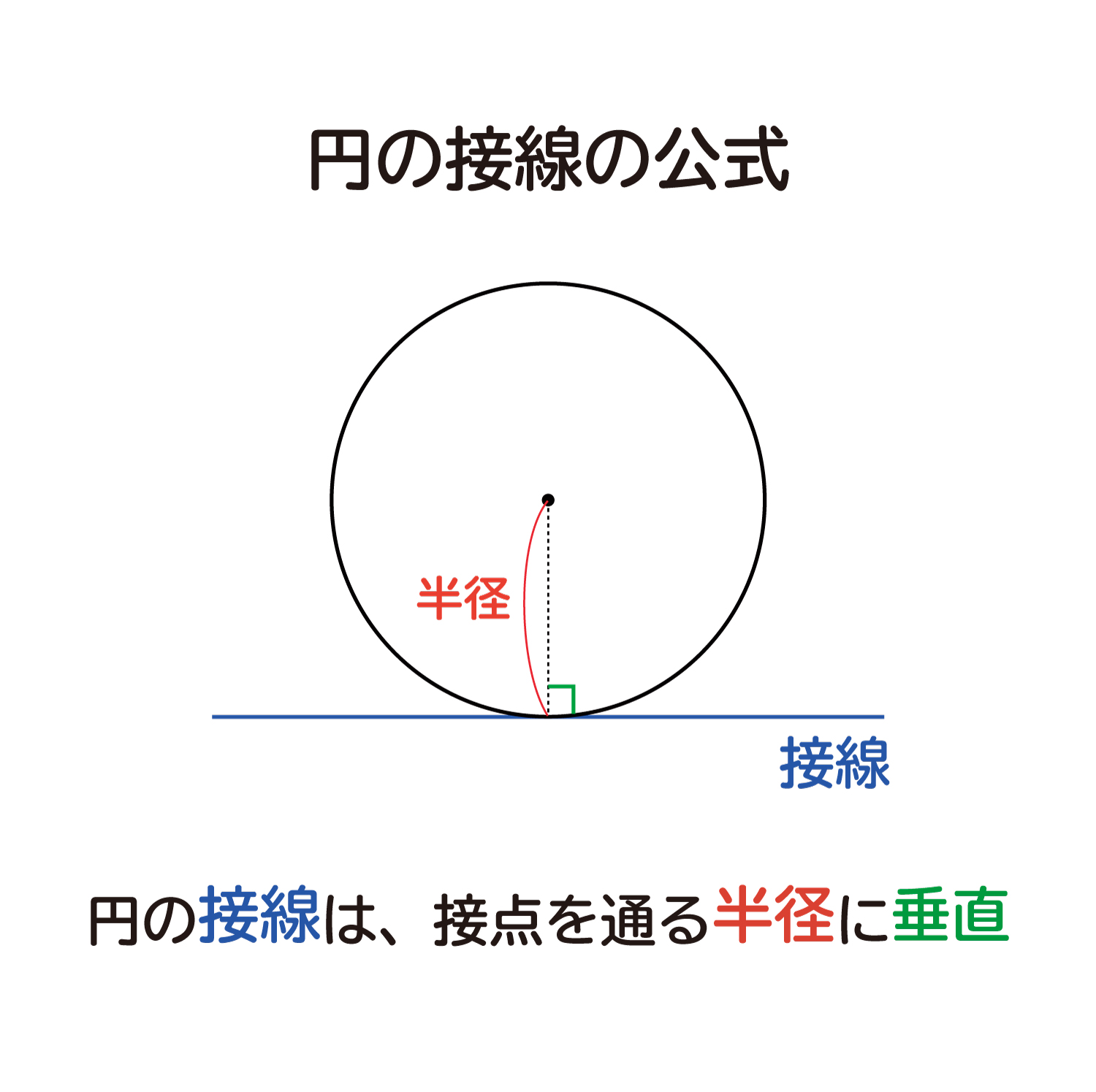
円の接線の方程式とその証明 おいしい数学

中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典

3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ

なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル

扇形 中心 角 求め 方

My Math Note

扇形 中心 角 求め 方

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary

楕円の知識まとめ 面積 方程式 焦点 接線 媒介変数表示 理系ラボ

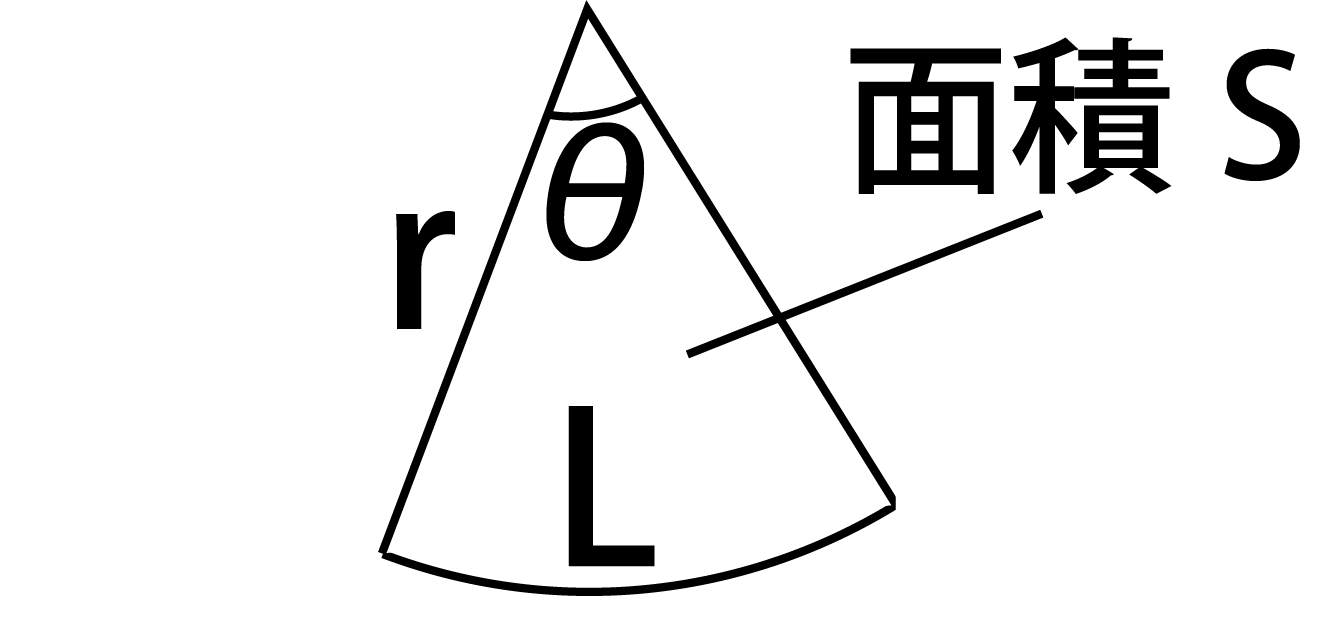
扇形 面積 求め 方

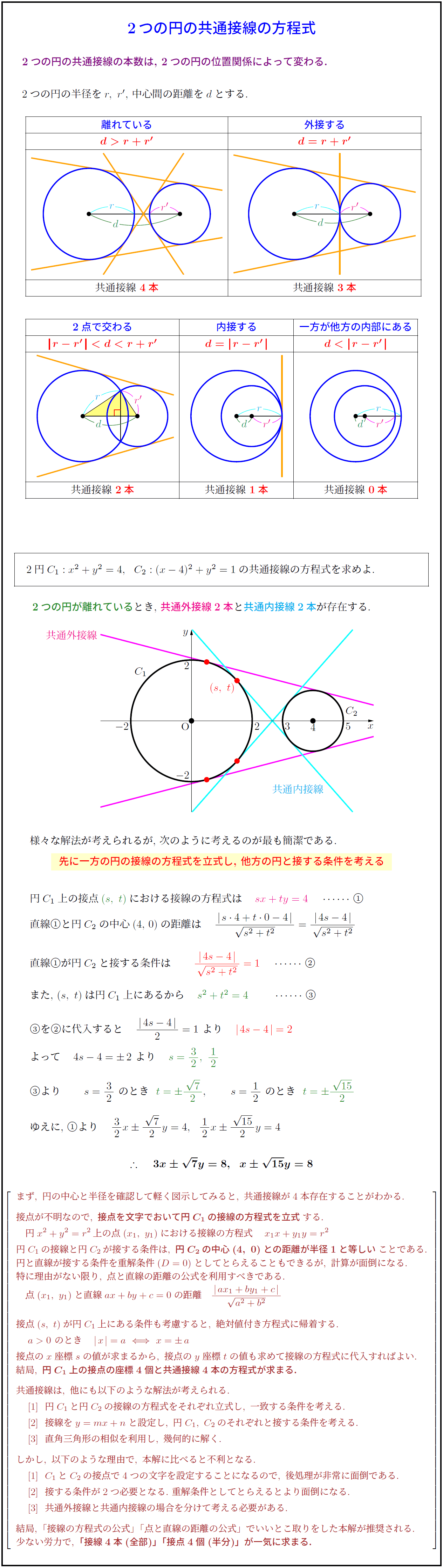
高校数学 2つの円の共通接線の方程式 受験の月

扇形面積 ラジアン 円の面積 円周 球の體積 表面積の公式の覚え方 微 Eoisg

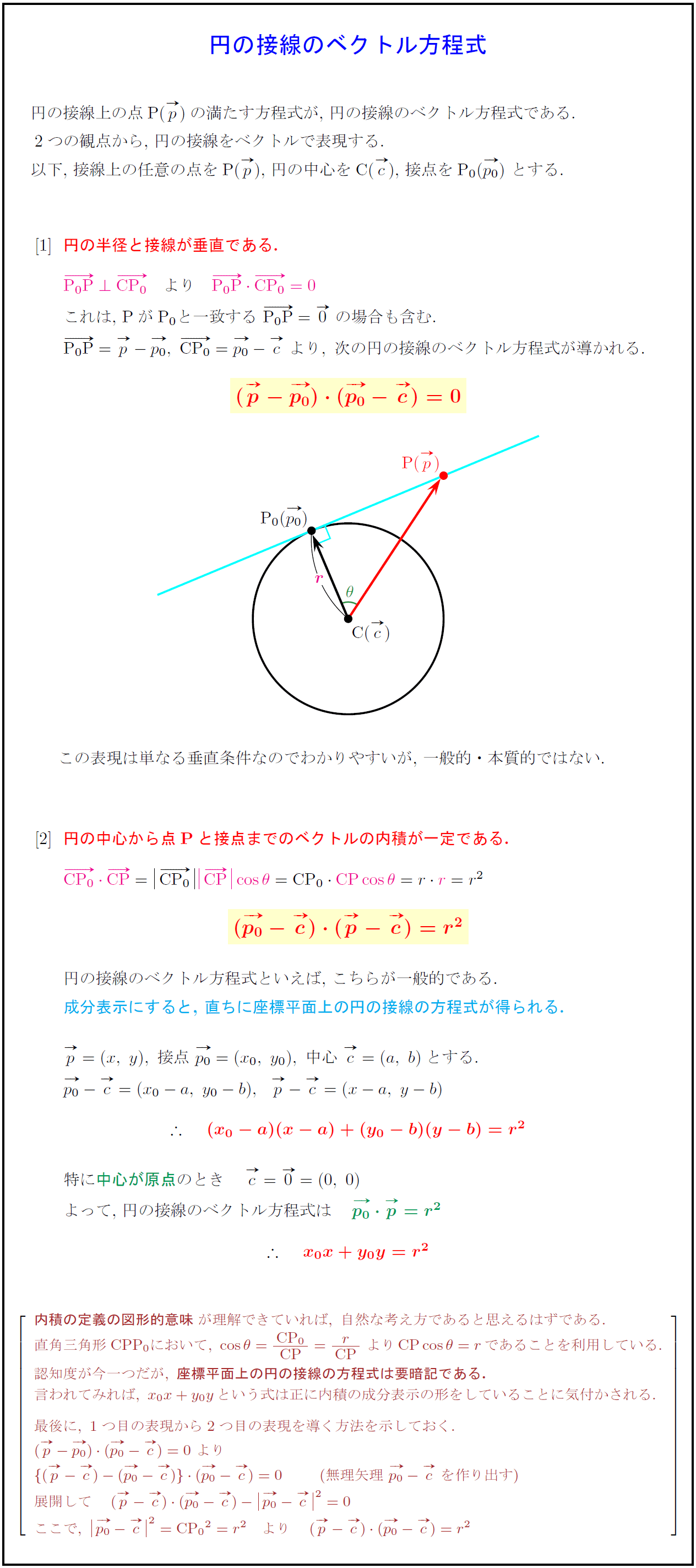
高校数学b 円の接線のベクトル方程式2パターン 受験の月

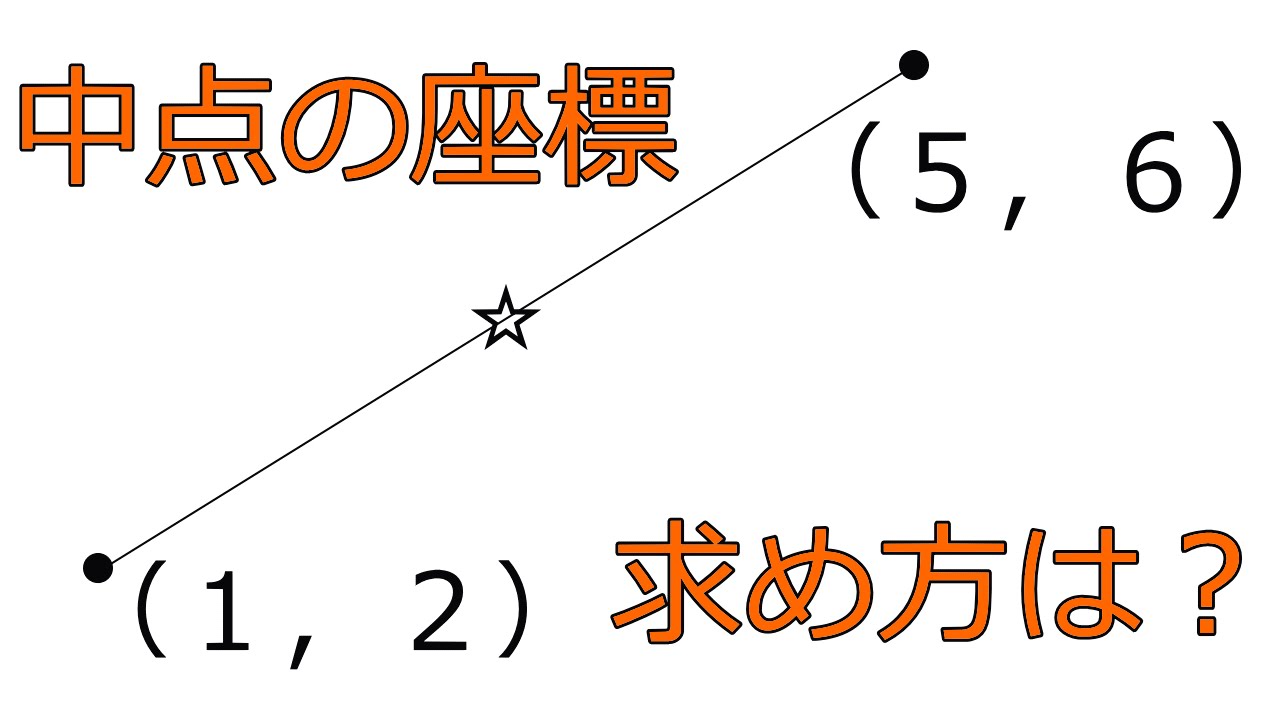
中点の座標の求め方 中学１年数学 Youtube

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

おう ぎ 形 中心 角 求め 方 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる

コンパスと定規を使った正方形 正四角形 の描き方 図形の描き方013a 夏貸文庫

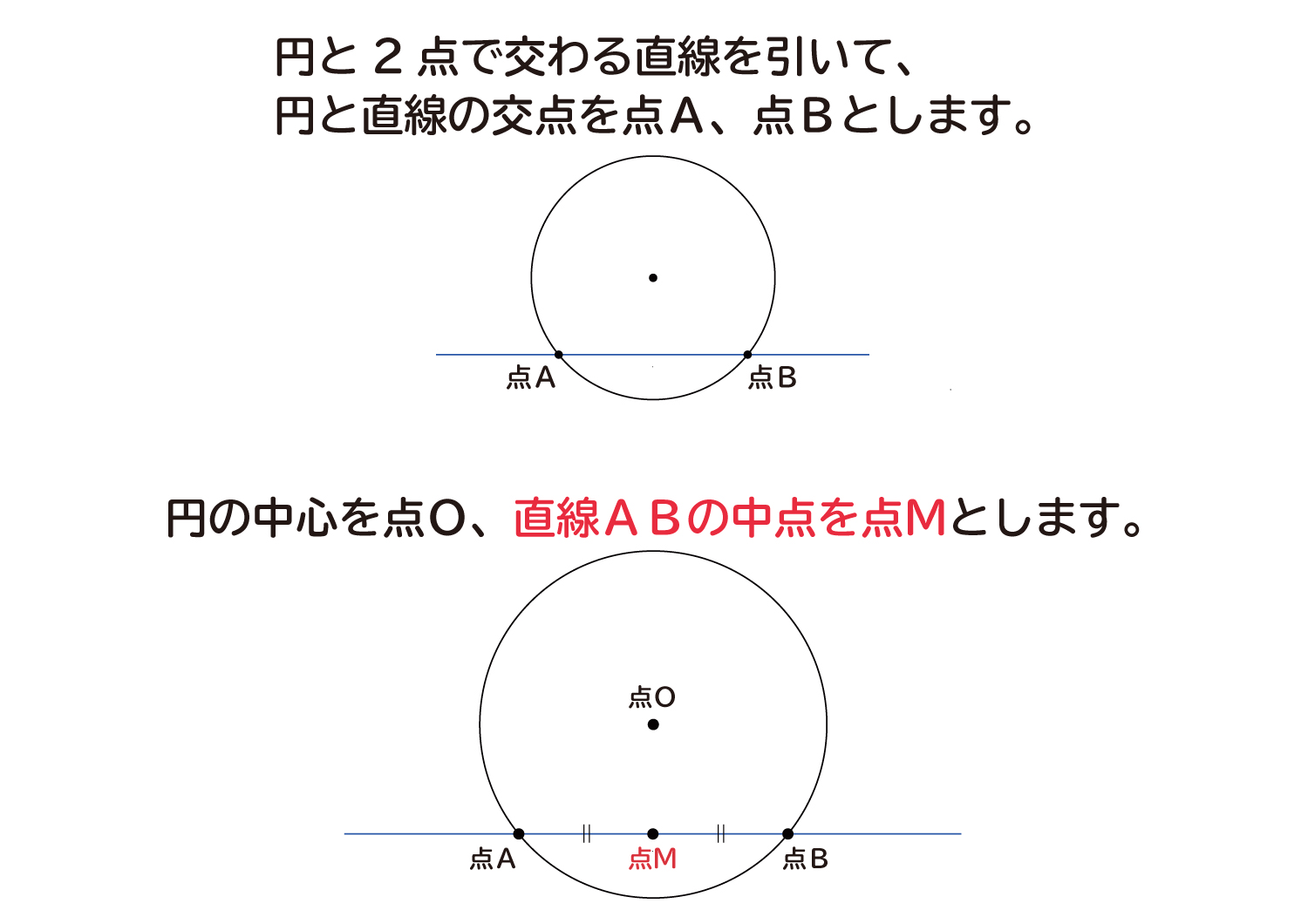
なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル

円の中心を求める 3つの方法 Wikihow

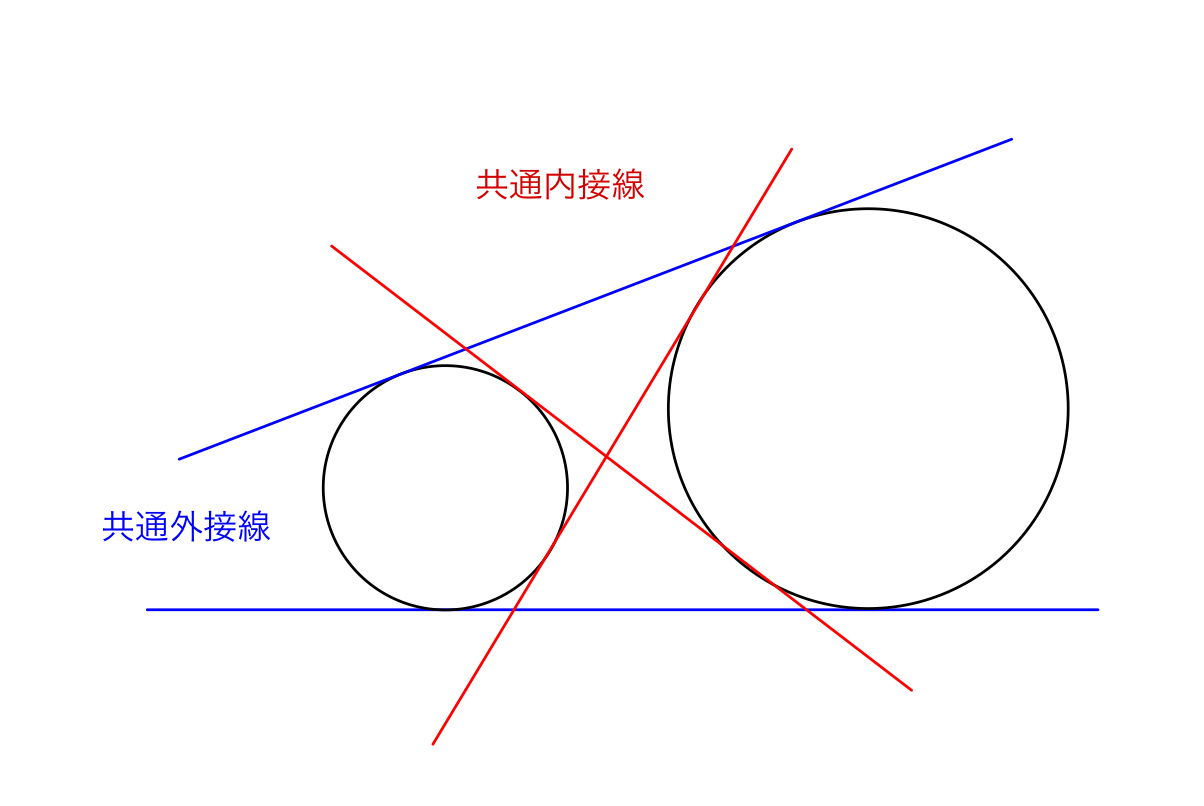
共通接線の問題5パターンの解き方を例題付きで解説 東大医学部生の相談室

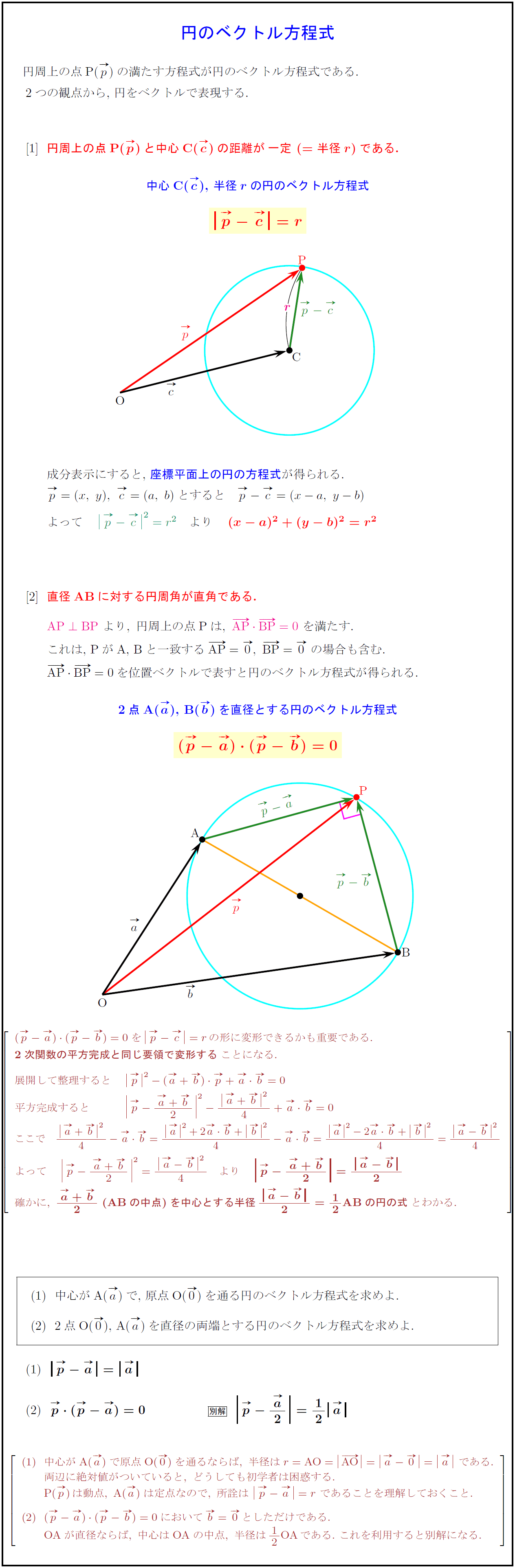
高校数学b 円のベクトル方程式2パターン 受験の月

極方程式の考え方と求め方 円と直線 高校数学の知識庫

X 1 2 Y 2 21 X Dfrac Descubre Como Resolverlo En Qanda

中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

円の中心からの角度から真円の円周上の座標を計算 座標早見表 Gamesprit

円と直線 切り取る線分の長さ 弦の長さ を求める問題を解説 数スタ

H28測量士試験過去問題解説 第10回 午前no 25 Geo Solutions 技術情報

台形 の 面積 の 求め 方 台形の面積の公式

円の接線の方程式とその証明 おいしい数学

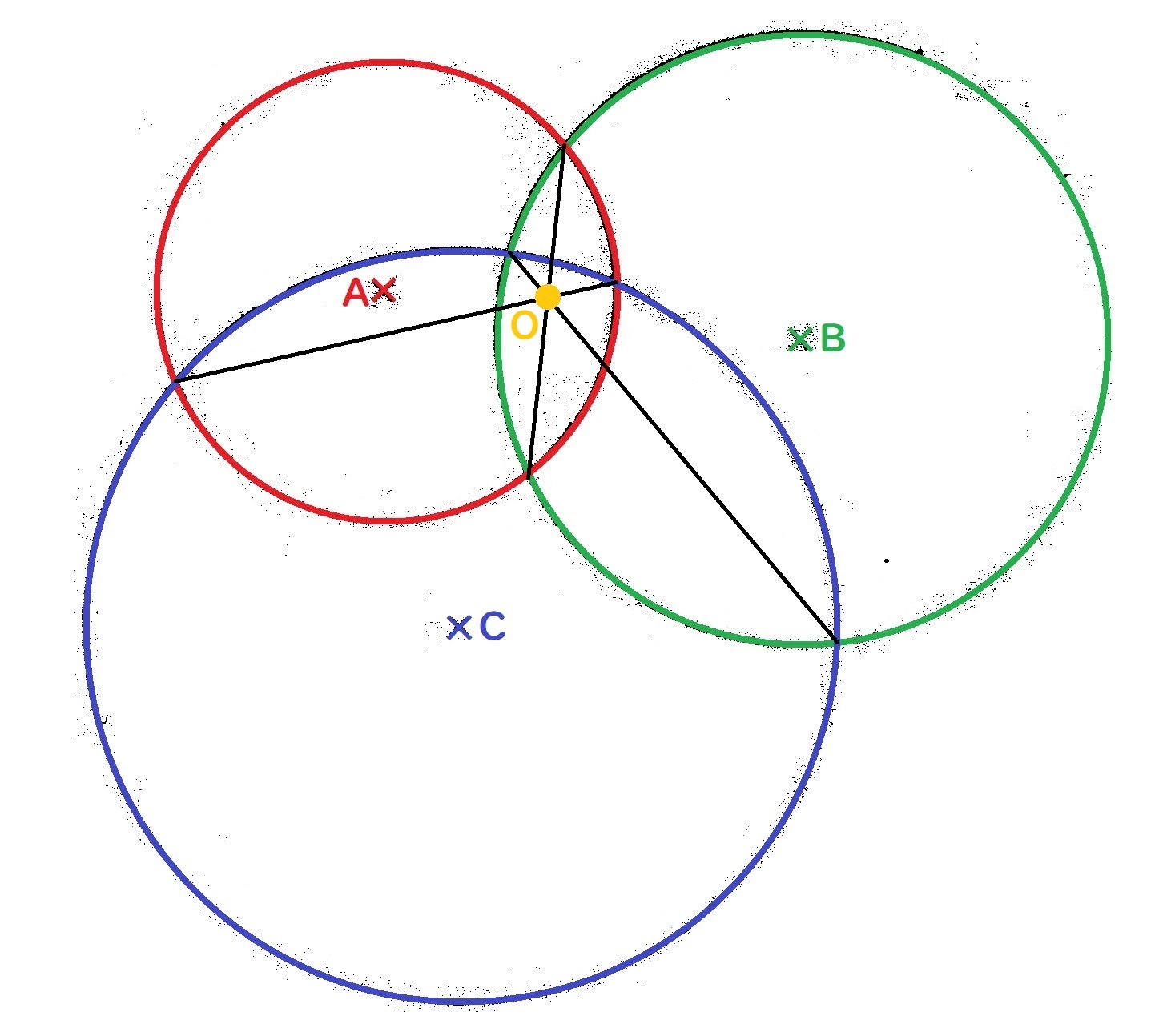
震源を探せ 作図編 理科とか苦手で

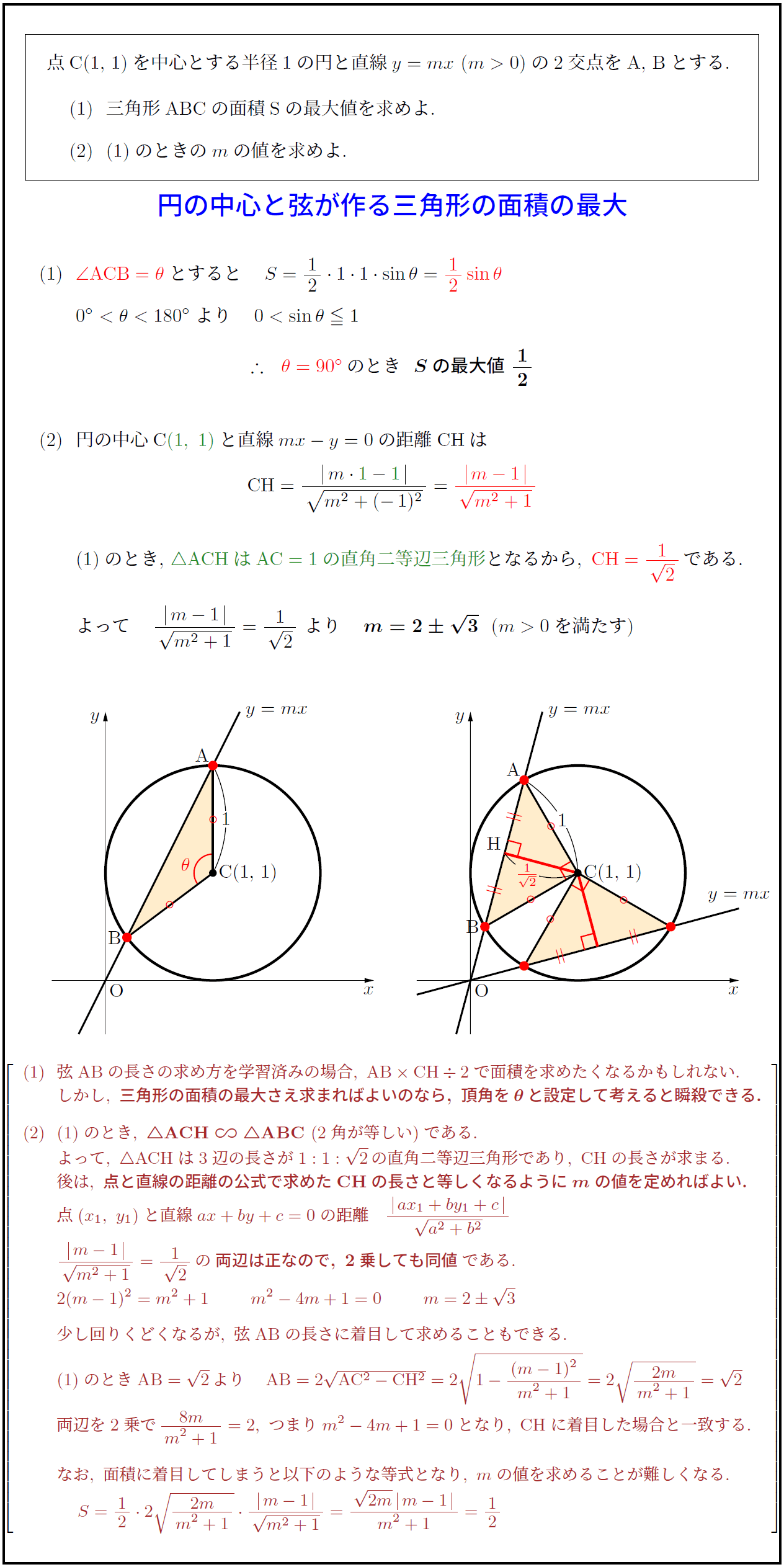
高校数学 円の中心と弦が作る三角形の面積の最大 受験の月

おうぎ形の中心角の求め方 Youtube

正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典

扇形 中心 角 求め 方

扇形 中心角 公式 学び 勉強 教科書

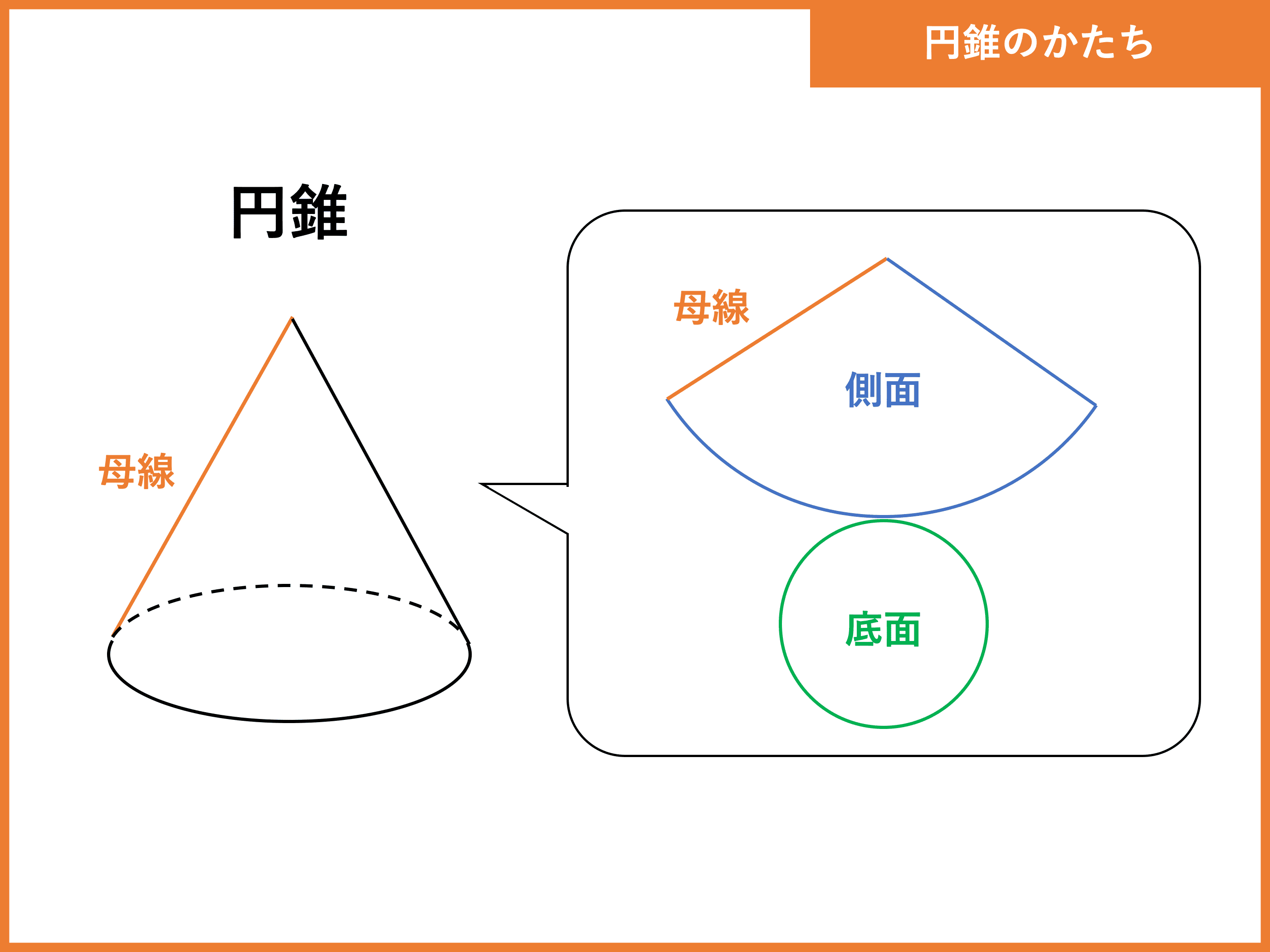
おう ぎ 形 中心 角 求め 方 おうぎ形の弧の長さ 面積 中心角の求め方と公式

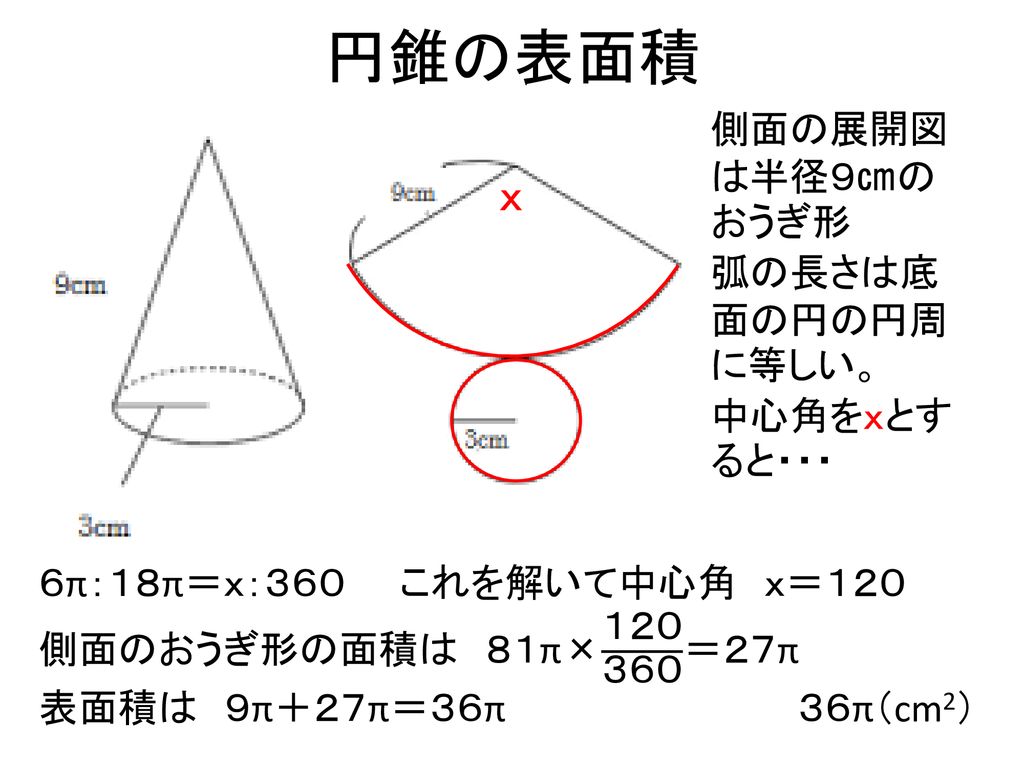
本時の目標 いろいろな立体の表面積を求めることができる Ppt Download

モールの応力円とは 意味と書き方を 計算をすっとばして説明するよ 超初心者向け のぼゆエンジニアリング

中心 角 の 求め 方

おうぎ形の弧の長さと面積の求め方 インターネット家庭教師のアスミラ

おう ぎ 形 中心 角 求め 方 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる

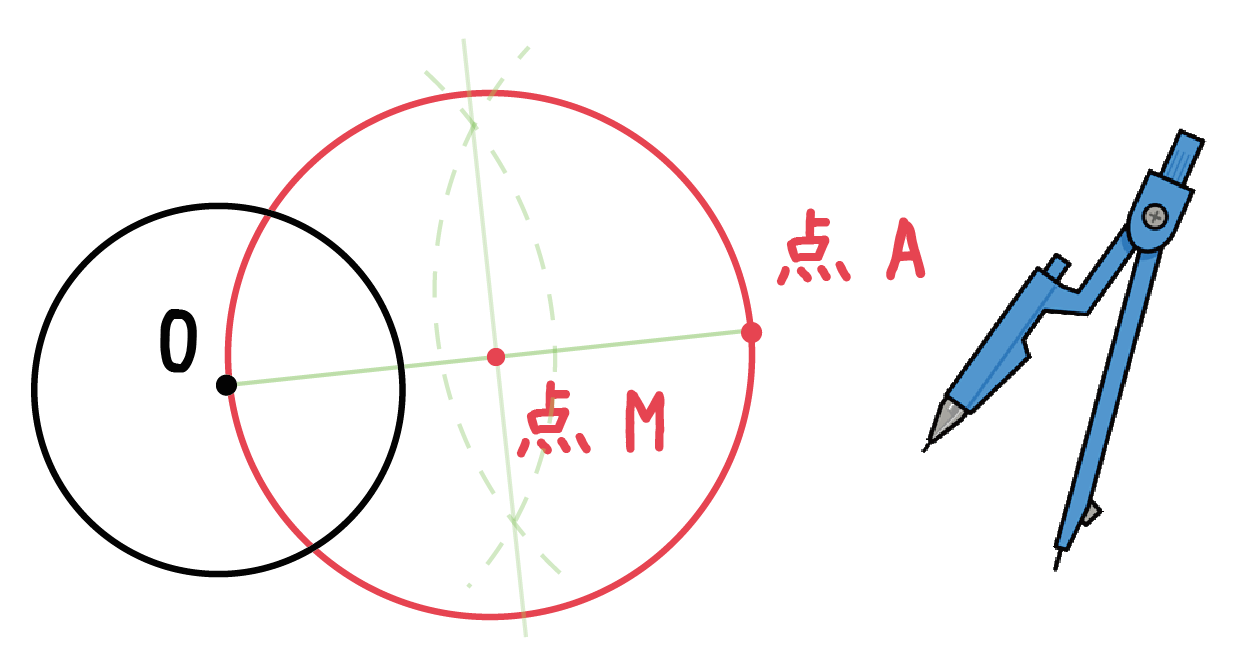
中１ 作図 円の中心を求める方法を解説 数スタ